Core Developer @ Hudson River Trading
On 7/7/2021, 6:49:33 PM
Section 3.5 of SICP is about streams, and I found this section absolutely fascinating (after never really understanding what a stream was). Incidentally, I happened to start reading A Gentle Introduction to Haskell at the same time as reading this section, and it is extremely satisfying to see the idea of laziness coincide.
Firstly, a quick review of the current place in SICP: chapter 1 covered procedural abstractions, chapter 2 covered data abstractions, sections 3.1-3 covered mutable state and the environment model (essentially imperative programming and how closures can be implemented), and section 3.4 covers concurrency. I think 3.4 is hastily thrown in, and it's also awkward because we aren't given the Scheme primitives to be able to implement the locking primitives. The only provided implementation is an implementation of test-and-set! on a uniprocessor; this would fail on a multiprocessor system (which most computers are nowadays, in which test-and-set! would normally be implemented as a hardware instruction (requiring a memory arbiter). 3.4 covers a lot of concurrency problems and approaches in summary, e.g., deadlocks and avoidance, memory barriers, "serializers" (what Java calls synchronized methods and what Tanenbaum calls "monitors" in Modern Operating Systems), locking primitives, and more. My opinion is that this material is better suited for a class in operating systems or distributed computing, and that the authors only hastily foisted it in here to demonstrate that imperative programming with mutation causes problems in the concurrent sense, or more generally, that introducing "time" into programs and variables, may be problematic. This also ties into the next section, in which streams are used to address the concurrency problem, as streams are "timeless."
Okay, back to streams.
We've done a lot with LISt Processing in LISP. Many of our algorithms are performed on lists or arrays of data, and often we only access data sequentially. Sometimes we can formulate this as a loop (or as tail-call recursion in Scheme), but sometimes the algorithm is more easily formulated as a list operation (e.g., map, filter, reduce) or aggregate expression (e.g., sum, max) on some meaningful list of data (e.g., the integers from 1 to 100, the Fibonacci numbers). Sometimes these sequences are common infinite sequences, and you want to only need to get values on some condition (e.g., integers up to 2 million, the first 50 prime numbers).
I tried to think of a creative example, but the example given in the book is great, if a little unrealistic. The proposed problem is to get the second prime in an interval. The naive way to do this, using list operations, is to generate the whole interval as a list, filter it for primes, and then choose the second value. But this generates an awfully large number of primes for which all but two (the first two) are important, and we may run of of memory if the interval is too large. An alternative approach is using iteration, but this is messy and we have to encode our logic into the loop.
The imperative programmer will probably think that the loop formulation is natural and efficient, but the functional programmer sees that using composable list operations is more readable and modular and not inefficient. But efficiency does become a problem when dealing with large lists, especially in cases when we do not use the entirety of the list, because the list operations we know (e.g., map, filter) take the entire list as input, process the whole list, and then return either a new list or an aggregate value as output. The more operations used, and the larger the size of the unused list, the worse the performance. An infinite list would be impossible both in time and memory.
This is where streams come in: we think of our algorithm as two operations: filtering by primes, and then retrieving the second value of the returned list. Ordinarily there may be many more operations in between. Since the input interval is arbitrarily large, we can think of it as infinite for our purposes. What we want to achieve is to only get as many primes as we need for this operation (2, as we want the second prime), and only get as many integers as we need (as many integers in the interval such that we retrieve two primes). In the example above, the second prime after 10000 is 10009, so we only need nine integers out of the input interval.
An additional goal is to interleave the operation, so that we do not have to store the intermediate lists all in memory at one time. Consider a modified scenario, in which we perform N separate map operations before filtering by primes and getting the second element. Imagine that in this scenario, we need M elements of the input interval, rather than nine, before finding the second prime. Then, between each map operation, we generate an M-element list. If we can find a way to interleave the map operations (which we can do by composing the mapped functions, but imagine that we mixed in different operations like map and filter which cannot be combined into a single list operation), then we only need to store N elements concurrently in memory rather than M. (M is much larger than N.) Note that this doesn't decrease the number of operations, but it decreases the memory requirement.
To achieve these (related) goals, we make the process "lazy": each of the intermediate lists only yield the next element "on demand." Another way to think of it is by working backwards: we know that we need exactly two primes, so we "ask" for two values from the primes list. The primes array then "asks" for elements of the integer list one at a time until we get two primes (asks 9 times). If there were more steps in this process, this "asking" process would continue. These "lazy" lists are then called streams. If we only "ask" for one value at a time from some list and have this "ask" propagate as needed in order to get the next value of that list, then the operations are naturally interleaved.
These "lazy" lists are called "streams," and they are beautiful. We get (roughly) the performance of iteration and the elegance of chaining modular operations. We can operate on infinite lists, because we only get as many values as needed; and operations are interleaved, which means that the used values of the streams can be discarded after use1.
If the practical side doesn't wow you, then perhaps you'll appreciate the observation that we can represent infinite data structures, or how simple it is to implement streams, or the power of only a few generic, composable stream operations, or the concision of implicit definitions of infinite streams.
Of course, we can't use regular lists to implement a stream. Unlike other languages where lazy evaluation is implemented by default2, function parameters are evaluated in full before invoking the function (applicative order evaluation).
What we need to implement a stream is delayed evaluation. We want to be able to "ask" for the next element of a stream without calculating the rest of the list. This is actually not hard: we can make each cdr of each cons in the list a thunk (a procedure that takes no arguments -- simply an expression that we can call later) that returns the next cons, which is of the same form. Thus each node of the linked list can be thought of as having a value cell and a "pointer function" (rather than a pointer) that gets the next stream element when needed.
While expressing streams by wrapping the cdr's in thunks works, it may be inconvenient for the user and more intuitive to express the stream like a normal list. Fortunately, in Lisp we have metaprogramming! We can use a simple macro to rewrite the cdr into a thunk when creating the list using cons3.
(define-syntax stream-cons
;; rewrite b into a thunk without evaluating it
;; for performance we would probably also want to memoize
;; the result in case it is used multiple times
(syntax-rules ()
([_ a b]
(cons a (lambda () b)))))
The rest of the stream primitives are fairly straightforward. Retrieving the next element of the list involves evaluating the cdr thunk.
(define *empty-stream* '())
(define stream-null? null?)
(define stream-car car)
(define (stream-cdr s) ((cdr s)))
Actually, you can see that stream-null? and stream-car are exactly the same as they are for normal lists. The only changes occur in the pieces related to the cdr.
To be explicit, you can see that the definition of stream-cdr is equivalent to invoking the cdr thunk:
(define (invoke t) (t))
(define stream-cdr (compose invoke cdr))
We can start by writing an operation akin to list-ref that gets the n-th element of a stream.
(define (stream-ref s n)
;; get the nth value of a stream
(if [zero? n]
(stream-car s)
(stream-ref (stream-cdr s) (1- n))))
We can define the typical list operations that produce another list, like filter, map, zip, running-sum, etc. just like we would with lists except that we use our new stream-* primitives.
(define (stream-map proc s)
;; stream equivalent of map
(if [stream-null? s]
*empty-stream*
(stream-cons (proc (stream-car s))
(stream-map proc (stream-cdr s)))))
The same is true of aggregate operations that produce a single value, such as sum, max, fold-left/fold-right, etc.
(define (stream-fold-left proc accumulator s)
;; stream equivalent of fold-left (left-associative accumulate)
(if [stream-null? s]
initial
(stream-fold-left proc
(proc (stream-car s) accumulator)
(stream-cdr s))))
Additionally, we may want to introduce certain operations that limit a stream. For example, the take operation returns a stream of a given length. We can also introduce a take-while operation that ends the stream when the predicate is not met. (Think of a filter operation, but it ends the stream when encountering a false value rather than dropping the element.) Similarly, we can discard elements of a stream so that we don't get values from the beginning of the stream. For this, we can introduce the skip and skip-while operators.
(define (stream-take n s)
;; take the first n elements of the stream
(if [or (stream-null? s) (zero? n)]
*empty-stream*
(stream-cons (stream-car s)
(stream-take (1- n) (stream-cdr s)))))
There are two types of stream operations (operations that take a stream as input): terminal and non-terminal (intermediate) operations. Non-terminal stream operations return another stream and allow you to chain and interleave streams and are thus lazy. Terminal stream operations do not output a stream, and are thus not lazy.
It is easy to tell what is an intermediate expression and what is not, because intermediate operations can composed in a "chain" and terminal operations can only appear at the end of a "chain"4. If we use the example from the book, we can now calculate the result efficiently in terms of stream operations (we will define the interval stream later):
(stream-ref (stream-filter prime? (stream-interval 10000 100000)))
In this case, stream-filter is an intermediate operation and stream-ref is a terminal one.
In the previous section, the operations that take an input stream and output another stream (e.g., stream-map, stream-filter, stream-zip) are lazy and thus non-terminal. When "asked" for a value, they lazily process their input stream in order to produce the next value. On the other hand, the operations that output some sort of aggregate value (e.g., stream-fold-left/stream-fold-right, stream-sum, stream-ref) must evaluate the entire stream before returning their aggregate value, and thus the input stream to these functions should be finite. We usually don't use streams directly, but usually use some aggregated value that is the result of a terminal operation.
Other examples of terminal operations, are stream->list, which converts a stream to a regular list, or stream-for-each, which eagerly loops through a stream.
(define (stream->list s)
;; terminal operation to convert (finite) stream to list
(if [stream-null? s]
'()
(cons (stream-car s)
(stream->list (stream-cdr s)))))
We can declare sequences as streams in the same way that we can lists (or infinite lists). All we need is some sort of (finite) generating function to find the next element.
Say, for instance, we wanted to generate the infinite stream of natural numbers (an example given in the book). We can do this by iteratively adding one to the previous element:
(define stream-natural
(letrec ([next
(lambda (n)
(stream-cons n (next (1+ n))))])
(next 0)))
The stream of natural numbers is useful in that we can use it to generate other sequences using an explicit formula5. For example, it is trivial to get the sequence of integer squares by mapping the square function over stream-natural, or to get the arithmetic sequence 3*x+1.
The function to generate the next sequence need not be so simple. We can use two previous elements, as is the case with Fibonacci (or three in the case of Tribonacci):
(define stream-fibonacci
(letrec ([next
(lambda (a b)
(stream-cons a (next b (+ a b))))])
(next 0 1)))
Or, we can include some logic, e.g., to generate a Collatz sequence.
(define (stream-collatz n)
(letrec ([next
(lambda (n)
(stream-cons
n
(cond ([= n 1] *empty-stream*)
([even? n] (stream-collatz (/ n 2)))
(else (stream-collatz (1+ (* n 3)))))))])
(next n)))
The method of giving an explicit formula for the next element based on the previous element(s) from the previous element is simple and intuitive, and we call this an explicit stream definition. However, we can also define streams implicitly, by starting with another stream and performing stream operations that output another stream. We've already seen this by mapping the stream of integers to another stream6.
Explicit streams are relatively bland. What I find really cool is that you can define streams fully in terms of itself in a "tail-chasing" manner, and that you can define streams that are interdependent and lazily "ask" each other for the next element.
For the tail-chasing variant, the simplest is a constant stream.
(define stream-ones
;; infinite stream of ones
(stream-cons 1 stream-ones))
This feels like a mathematical definition that shouldn't be possible in code, but it works because of the delayed evaluation. A more complicated example is the integers. We've already defined it with an explicit recursive function based on the previous element, but we can also define it in the following way (we require the stream-add helper and the variadic form of stream-map, whose implementation is not shown above):
(define (stream-map proc . argstreams)
;; generalized (variadic) version of stream-map
;; assumes all input streams are the same length, or
;; at least that the first one is the shortest stream
(if [stream-null? (car argstreams)]
'()
(stream-cons
(apply proc (map stream-car argstreams))
(apply stream-map
(cons proc (map stream-cdr argstreams))))))
(define (stream-add s1 s2)
;; add two streams
(stream-map + s1 s2))
(define stream-natural
;; an implicit definition of the stream of natural numbers
(stream-cons 0 (stream-add stream-natural stream-ones)))
This is already very nice and concise, but we can do better without even requiring stream-add or stream-ones.
(define stream-natural
;; an even more concise definition of the natural numbers
(stream-cons 0 (stream-map 1+ stream-natural)))
We can do a similar thing with the Fibonacci numbers:
(define stream-fibonacci
(stream-cons
0
(stream-cons
1
(stream-add
stream-fibonacci
(stream-cdr stream-fibonacci)))))
The example of the infinite stream-ones stream was intuitive to me immediately, but it took some time to understand how this works and it blew my mind when I understood it.
We generate the n-th element of the inner stream-add sequence by taking the sum of the n-th element of the stream-fibonacci sequence and the n-th element of the (stream-cdr stream-fibonacci) sequence. Hovewer, the inner stream-add is exactly equivalent to (stream-cddr stream-fibonacci), so it begins to map over the elements of itself. All we need are some starting initial values, and then the map operation "chases its own tail" by mapping over previous elements of the same stream.
The following diagram, from A Gentle Introduction to Haskell (which will be discussed in the next section), was helpful for my understanding.
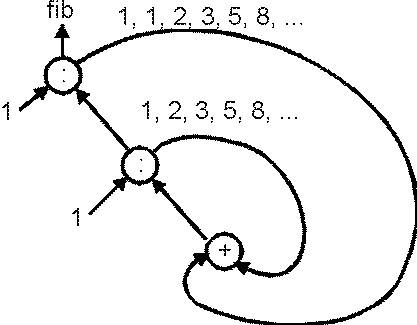
I will save the example of the interdependent streams to the end of this post because it's a little hairier.
Streams vs. Javascript (RxJS)I actually read the Chapter 3: Functions of A Gentle Introduction to Haskell the day before reading the streams section in SICP, without knowing that they would both relate to streams.
In Haskell, though, we don't call them streams -- they're just regular lists. It's the default, nothing out of the ordinary. The term "non-strict" and "strict" are used instead of "lazy" and "eager," and the equivalent of the cons operator in Haskell is non-strict by default.
They give implicit versions of the stream-ones, stream-natural, and stream-fibonacci streams. The Fibonacci example is presented like so, using the zip primitive rather than the stream adding operator.
ones = 1 : ones
numsFrom n = n : numsFrom (n+1)
fib = 0 : 1 : [ a+b | (a,b) <- zip fib (tail fib) ]
This kind of definitions makes me want to fall in love with Haskell.
Take the other extreme: a classically imperative language that tries to implement streams. Java.
Java 8 made big steps towards FP because of the introduction of lambda expressions (syntactic sugar for their terribly clunky "functional interfaces") and because of the introduction of streams, which was probably only possibly with a usable lambda syntax.
I haven't used Java streams much. Java 8 came out around the same time that I began learning how to program computers, so I thought that those new features might be some obscure thing I would never use. Looking back on it, it looks like Streams are mostly used to chain list operations and allow for parallelism. You can easily split a stream for concurrent processing because the iterator is a Spliterator, and you can perform the common list/stream operations like map, filter, and reduce.
I tried to see if Java has a way to elegantly write implicit streams in terms of themselves like you can in Haskell or Scheme, and I don't think you can (as far as I can tell from moderate Internet search). The most elegant stream implementation of Fibonacci I can find is by using pairs, which is hardly elegant because this ends up just being an explicit definition of the sequence, not to mention that we're duplicating every term of the sequence:
Stream.iterate(new int[]{0, 1}, t -> new int[]{t[1], t[0] + t[1]})
.limit(10)
.forEach(x -> System.out.println("{" + x[0] + "," + x[1] + "}"));
Similarly, I went to see if we could do something similar to the Haskell edition by using a zip operator, but it seems that it's not elegant at all to implement the zip operator, or to be able to interleave two streams. My guess that this inconvenience is due to how the Spliterators are implemented internally, which I speculate is probably implemented similar to a loop. While this might make streaming over a single list easy and wouldn't inhibit splitting a single list, it would make combining two lists difficult7.
Other annoyances of Java streams are that you can only use them once8, and that you must pass in a lambda (or functional interface if you prefer to be verbose) rather than an expression, if you want to specify a sequence explicitly. There are no Java macros to rewrite that expression into a delayed expression, so you have to do it yourself.
I want to bring up one more implementation of streams: the RxJS library (Reactive eXtensions for JS). This is where I first learned about streams. More specifically, it supports the "reactive programming" paradigm, which is, according to Wikipedia, a programming paradigm "concerned with data streams and the propagation of change." This is very useful in Javascript, where many actions are event-driven. The basic data type is the Observable, to which other objects can "subscribe" to. These subscribers then can use stream-processing operators to process the incoming events. I highly recommend this library.
I will preface this by saying that I don't understand this topic too well, but it seems to be another fundamental reason why we use streams. By their nature, streams are immutable. We never change the values in the memory cells of the underlying linked list; all we do is generate new elements (and discard old ones by means of garbage collection). Thus we have no chance for race conditions.
What I understand is that this falls well under the immutable paradigm that is present in functional programming. As a result, much of the time streams are associated with parallel and concurrent processing. Take, for example, the default iterator for a Stream in Java. It is the Spliterator, which, as the name suggests, naturally handles splitting into parallel streams. From what little I've heard about Clojure (the JVM-based Lisp), it is a great language for concurrency because of its support for parallel streams.
I've still yet to find a compelling example of this because I don't often deal with hardcore parallelism or streams, so this is just speculation.
Often, we need to make a search over some half-interval (e.g., the the natural numbers) for numbers matching some criteria (e.g., the first ten prime numbers). We can simply iterate over this infinite stream.
The problem gets more complex once we move to multidimensional data. Say we want to search the space of the quarter-plane of the Cartesian product of the natural numbers9? Or a search over a whole plane (e.g., the complex numbers)? Or even a 3-D space? The problem here is that there is no implicit ordering in these elements.
One way to approach this is to break down the problem into multiple infinite (1-D) lists (streams). In the example of the Cartesian product, we have an infinite stream of pairs beginning with 0, a stream of pairs beginning with 1, and so on. And then we need to take the union of these streams, but concatenation is not an option, since we will never complete the first stream.
As a result, we need some way to merge the streams such that each element of each stream will be reached in some finite time10. The simplest method is interleaving, and an implementation is shown in SICP. However, this will likely not be the "fairest" or most efficient method of merging for a particular problem. Thus, the best method of merging infinite lists may be specific to each application and an important performance consideration.
One of the things that Prof. S and I noticed is that Abelson and Sussman sometimes get extremely and unnecessarily philosophical. One example is in the beginning of chapter one when talking about wizards11. Or when they discuss the idea of "sameness" in the beginning of chapter 3, or when they discuss the theory of relativity and that "our computational models may in fact mirror a fundamental complexity of the physical universe" when talking about concurrency. In the same way, this section of streams is wrapped up with a discussion of streams as a way of modeling objects "without time" in the FP sense, as opposed to with "with time" as with mutation and imperative programming12.
While the philosophical elements are a little over my head, I do want to talk about the practical side to this.
So far, what I've been focused on is the benefits of using streams for iteration. We get the nice benefits of theoretically infinite lists and modular list operations, with good time and memory efficiency due to laziness and interleaving of operations. In this section, we interpret streams as a data model rather than a computational model.
Abelson and Sussman return to the example from the beginning of the chapter about the "bank account" model, in which we have essentially an object that contains a mutable "balance" field. The authors propose that we rewrite this in terms of a list or stream of operations: rather than performing one operation at a time and observing the change in balance, we instead input a stream of operations and return a stream of balances after applying those transactions. In this way, they claim, the operation becomes pure and stateless: rather than depending on some local, mutable state, we treat the stream of operations as a single entity and operate on that entity as a whole. My interpretation of what "timeless" means in this context is that we have flattened operations over time dimension into the memory dimension.
One qualm about this is that we don't solve the concurrency problem, but we rather abstract it away by stating that there is a clear order of transactions. I'm not sure if that's the intent of the authors here, though.
As another, very similar example, we have the random number generator, which (at least for a LCG) needs to hold state. Rather than storing the state as a mutable element, we can store the values as an infinite stream13 of the internal state. I'm not sure if there's really any practical benefit of this over the mutation version; this is simply the FP version of the PRNG.
In general, I can see myself using streams in this way, but I'm more interested in the elegance and performance of stream processing. I appreciate that we get a pure function of the input stream, but I need to see an example that will convince me of its benefit. The main practical benefit I can think of of storing a mutable object's state over time is that we can keep track of the history of an object like we can in Redux. Due to structural sharing and referential transparency, efficient memory allocation and change detection is given for free.
I already mentioned this when I was talking about implicit stream definitions. This is the implicit definition of two streams -- based off of one another, which is even cooler. When defining a stream implicitly in terms of itself, we had to define an initial term (or two, in the case of Fibonacci); we have to do the same in the case of interdependent streams, because one stream has to be able to ask the other for a value in order to produce an initial value to get the process started.
The example given by the book is a differential equation solver, which is a perfect use case. We achieve this by choosing one sequence to be the initiator -- it takes an initial value and take the second stream as a delayed input.
This example is cool but I can't add much value in reproducing it here. This is the example from section 3.5.4.
I'll preface this with saying: this is not the sieve of Eratosthenes, as the authors claim. It's a neat prime sieve expressed in terms of streams, but it is fundamentally less efficient. There is a paper that explains why this example is not esieve. It seems that this particular example is common amongst people who advocate FP, but it seems that there isn't really an efficient way to implement a esieve without mutation (the authors suggest using a priority queue, which is fundamentally an array-based data structure).
It is still a cool example, so I'll include it here.
(define (sieve stream)
(stream-cons
(stream-car stream)
(sieve (stream-filter
(lambda (x)
(not (divisible? x (stream-car stream))))
(stream-cdr stream)))))
(define primes (sieve (integers-starting-from 2)))
I think this is really cool. One result from calculus is that an alternating series with terms diminishing in absolute value converges. The Euler transform is a stream operation that maps a sequence of partial sums to a different sequence of partial sums that converges more quickly.
If \(S_n\) is the n-th term of the original sum sequence, then the accelerated sequence has terms \(E_n=S_{n+1}-\frac{(S_{n+1}-S_n)^2}{S_{n-1}-2S_n+S_{n+1}}\).
(define (euler-transform s)
(let ((s0 (stream-ref s 0)) ; S_{n-1}
(s1 (stream-ref s 1)) ; S_n
(s2 (stream-ref s 2))) ; S_{n+1}
(cons-stream (- s2 (/ (square (- s2 s1))
(+ s0 (* -2 s1) s2)))
(euler-transform (stream-cdr s)))))
Even more magically, since the transformed sum is also a sequence of partial sums of an alternating sequence, we can accelerate the accelerated sequence recursively, until we run out of machine precision. I won't repeat their example, but they implement this using a "tableau" data structure -- a stream of streams.
I don't know how this magic works, and this isn't especially related to streams, but it's very cool and works amazingly.
1. Theoretically, but this will be performed by the garbage collector and the memory reclamation will not be perfect. I tested this out on infinite streams with Chez Scheme, and the garbage collection couldn't keep up with the "garbage disposal."
2. e.g., Haskell, where laziness is the norm and strictness is optional.
3. SICP states that the delayed evaluation is achieved by wrapping the code in thunks, but does not mention macros even though this seems the obvious solution. I don't know why.
4. Sometimes this "chain" of stream expressions is referred to as a pipe, as it is in the Javascript RxJS library, but for us it is simply function composition.
5. A formal definition of a sequence may be a function from the natural numbers into the set of possible elements of the sequence.
6. The terms "implicit" and "explicit" are just handy ways of describing our stream definitions, but the definitions of these terms may be a little arbitrary. I use the word "explicit" to mean that a recursive formula is given to generate the next element, while the word "implicit" to mean any stream that is not "explicit." I bring this up because we can define sequences using "recursive formulas" or "explicit formulas," in which case "explicit" here means an explicit function of the sequence of natural numbers. Thus, the definition I use of "explicit" streams is exactly the definition of "recursive" sequences, and my use of the word "implicit" streams includes but is not limited to "explicit" sequences (which can be formed by applying the stream map operation over the stream of natural numbers). It is not limited to "explicit" sequences because we can also define some "recursive" sequences "implicitly," such as the Fibonacci sequence. And of course, we can sometimes define a stream or sequence in either an explicit or implicit manner, just like how we can sometimes define a sequence explicitly or recursively, and then the term describes the manner in which we describe the sequence rather than describing the sequence itself. But I digress.
7. This is based on my intuition, so it may be wrong. Whatever the case, the fact is that it's awkward to implement streams in Java with the flexibility and intuitiveness that you can in a more funtional language.
8. This supports my hypothesis that streams are implemented like loops, in which the used values are discarded. This is unlike in Haskell or Scheme, where the stream is fundamentally an ordinary linked list in memory.
9. The list of pairs (0,0), (0,1), (1,1), (0,2), (1,2), (2,2), ...
10. This characterization may not be entirely mathematically correct. I'm not experienced when talking about infinity.
11. Perhaps this is practical in that it earns the book its cover image and its nickname, the "Wizard book."
12. They conclude this section and the third chapter by stating that a grand unification of these two models has yet to emerge, which sounds a little too grandiose for me.
13. LCGs are not actually infinitely-repeating, but we can approximate them to be.
© Copyright 2023 Jonathan Lam